Les pavages

A) Qu’est-ce-qu’un pavage ? Comment peut-on en construire ?

1) La définition d’un pavage

Pour comprendre ce qu’est un pavage, il faut d’abord savoir ce qu’est une tuile.
Il s’agit d’un motif plan sans trou, qui sert de base au pavage, comme un carreau servant à carreler le sol.
Un pavage est un recouvrement périodique du plan à partir d’un nombre fini de tuiles, sans superposition ni espace vide.

 

 

Sur l’image de gauche, une tuile est un motif vert, orange ou rose. À droite, il s’agit d’un motif vert ou orange. Les tuiles peuvent avoir des formes très variées comme vous pouvez le constater ici ainsi que dans tous les autres pavages. (Source des images : serge.mehl.free.fr)

On applique à la tuile choisie des isométries planes, qui sont les transformations du plan qui conservent les distances et les angles non orientés. Petit à petit, on recouvre tout le plan.

2) Les transformations utilisées

Parmi toutes les isométries planes, celles grâces auxquelles on peut construire un pavage sont :

• les translations,
• les rotations à 60°, 90°, 120° et 180°,
• les symétries axiales,
• les symétries glissées (qui sont les composées d’une symétrie axiale et d’une translation).

En combinant ces isométries, on peut construire différents types de pavages.
On peut penser qu’il est possible d’obtenir un très grand nombre, voire une infinité, de pavages. En fait, ce n’est pas le cas pour deux raisons :
– toutes les combinaisons des isométries ci-dessus ne permettent pas de créer un pavage.
– certaines combinaisons a priori différentes donnent en réalité le même résultat.

Étudier les différents types de pavages et les dénombrer est un problème mathématiquement très intéressant, mais bien qu’on connaisse les pavages depuis l’Antiquité (leur utilisation dans différentes œuvres d’art en témoigne), ce n’est qu’en 1891 que le cristallographe et mathématicien russe Evgraf Fedorov a démontré qu’il n’en existait que dix-sept types.

B) Quels sont les différents types de pavages ? Comment peut-on les différencier ?

1) Les dix-sept types de pavages

Il existe dix-sept types de pavages qui sont caractérisés par les transformations par lesquelles ils sont engendrés.
Comprendre la classification des pavages n’est pas très simple, nous vous conseillons de vous pencher d’abord sur les frises.
En effet, un pavage est une structure plane (de dimension 2) alors qu’une frise est une structure linéaire (de dimension 1). Les frises sont plus simples à étudier que les pavages et vous permettront de comprendre pourquoi certaines transformations combinées en engendrent toujours d’autres.
Pour cela, nous vous conseillons la vidéo de MicMaths sur les frises. Vous découvrirez pourquoi il n’en existe que sept types.

Nous vous recommandons également cette autre vidéo de MicMaths dans laquelle vous verrez les liens entre les frises (de dimension 1), les pavages (de dimension 2) et les cristaux (de dimension 3).

Une remarque importante avant de présenter les dix-sept types de pavages : deux pavages peuvent sembler différents mais être du même type. Ce n’est pas l’aspect esthétique qui compte, mais uniquement les propriétés mathématiques.
Par exemple, les deux pavages ci-dessous sont du même type, ce sont des P1, le premier type que nous allons vous présenter. (Source des images : serge.mehl.free.fr)

Voici la liste des dix-sept types de pavages avec les isométries utilisées pour les obtenir. Les translations ne sont pas mentionnées car tous les pavages en comportent dans au moins deux directions.
J’ai volontairement mis deux illustrations pour chaque type de pavage. Celle de gauche vous permet de mieux visualiser les tuiles tandis qu’à droite, les motifs vous permettent de comprendre plus facilement les transformations utilisées. Dans les images de droite il est parfois difficile de discerner les tuiles.
Dans le P4, le carré noir représente une tuile. En effet, il ne s’agit pas simplement d’une tasse car cette forme ne permet pas de paver le plan mais une tuile est un carré dans lequel est dessiné une tasse. C’est le cas pour tous les pavages de droite : une tuile n’est pas le motif seul, mais une forme géométrique (carré, triangle…) qui l’inclut et qui contient donc du blanc autour du motif.

1. Le P1 comporte uniquement des translations.

2. Le P2 comporte 4 rotations de 180°.

3. Le P3 comporte 3 rotations de 120°.

4. Le P4 comporte 2 rotations de 90° et 2 rotations de 180°.

5. Le P6 comporte une rotation de 60°, une rotation de 120° et une rotation de 180°.

6. Le PG comporte une symétrie glissée.

7. Le PGG comporte 2 symétries glissées et 2 rotations de 180°.

8. Le PMM comporte 2 symétries axiales et 4 rotations de 180°.

 

9. Le CM comporte une symétries axiale et une symétrie glissée.

10. Le P4G comporte 2 symétries axiales, 4 symétries glissées, 2 rotations de 90°, 2 rotations de 180°.

11. Le P3M1 comporte 3 symétries axiales, 3 symétries glissées, 3 rotations de 120°.

12. Le P31M comporte 3 symétries axiales, 3 symétries glissées, 2 rotations de 120°.

13. Le P4M comporte 4 symétries axiales, 2 symétries glissées, 2 rotations de 90°, 2 rotations de 180°.

14. Le P6M comporte 6 symétries axiales, 3 symétries glissées, une rotation de 60°, une rotation de 120° et une rotation de 180°.

15. Le PM comporte une symétrie axiale.

16. Le PMG comporte une symétrie axiale, une symétrie glissée et 2 rotations de 180°.

17. Le CMM comporte 2 symétries axiales, 2 symétries glissées et 4 rotations de 180°.

(Source des images : serge.mehl.free.fr à gauche et « Deux (deux ?) minutes pour… classer les pavages ! » de El Jj https://www.youtube.com/watch?v=N5DGzm7xHRA à droite)

  2) La clé de détermination des pavages

Lorsque l’on regarde un pavage, il n’est pas facile de déterminer à quel type il appartient. Pour cela, on utilise une clé de détermination. Elle fonctionne sur le même principe que celles utilisées en biologie : il s’agit d’une succession de choix d’alternatives portant sur les caractéristiques de l’objet étudié.
Il existe différentes clés permettant de classer les pavages.

Avec la clé ci-dessous, demandez-vous d’abord si le pavage comporte ou non une rotation. Si c’est le cas, demandez-vous ensuite quel est le plus petit angle de rotation. Sinon, demandez-vous s’il existe au moins une symétrie axiale. Et ainsi de suite, jusqu’à ce que vous arriviez à la dernière ligne : vous avez alors terminé et vous savez de quel type est le pavage étudié.

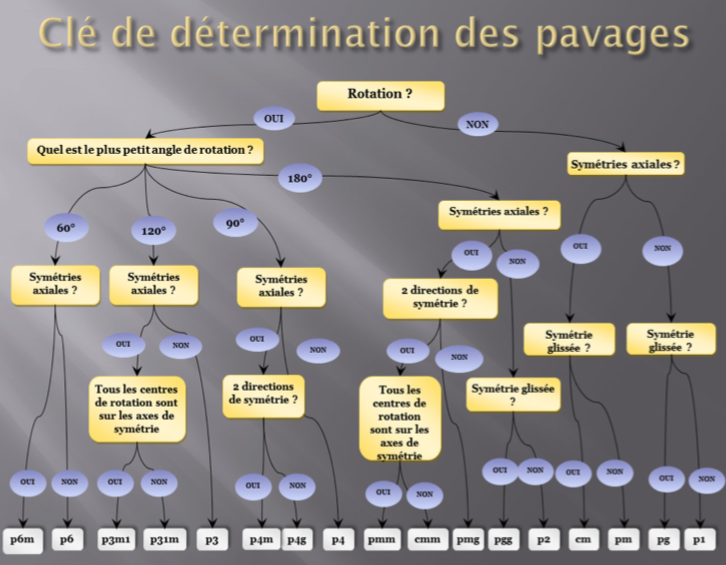
(Source de l’image : https://www.mathenjeans.fr/sites/default/files/17_pavages_a_lalhambra_college_henri_wallon_marseille.pdf)

3) Construction d’un pavage avec GeoGebra

Voici une vidéo dans laquelle je réalise un pavage avec des rotations de 120°, en partant d’un hexagone régulier que je déforme afin d’obtenir une tuile plus originale.

À vous de jouer !

Maintenant, c’est à vous de retrouver à quelle famille appartiennent ces pavages d’Escher. (Ne regardez pas trop vite les solutions qui sont en-dessous !)

Solutions

Le premier pavage est un PG. Il ne comporte ni rotation ni symétrie axiale mais possède une symétrie glissée.
Le deuxième est un PGG car son plus petit angle de rotation est 180° et il ne comporte pas de symétrie axiale, mais il possède une symétrie glissée.
Le troisième est un P1. Il ne comporte ni rotation, ni symétrie axiale, ni symétrie glissée.
Le quatrième est un P6 car son plus petit angle de rotation est 60° et il ne compte pas de symétrie axiale.

J’espère que cette présentation des pavages vous a intéressés.
Escher a également réalisé des pavages plus complexes que ceux que je vous ai présentés. Afin de les analyser, il faut regrouper plusieurs motifs en une seule tuile.
À gauche, une tuile est composée d’un homme blanc et d’un homme noir tandis qu’à droite, une tuile est constituée d’un oiseau blanc et d’un oiseau bleu. Attention, il y a plusieurs façons de choisir la tuile. Par exemple pour l’image de droite, vous pouvez choisir d’associer un oiseau blanc avec l’oiseau bleu qui se trouve en haut à sa gauche ou avec celui situé en bas à sa droite.

 

 

Enfin, Escher a réalisé des pavages d’un autre type qui sont dits non-périodiques. Cela signifie qu’on ne peut pas trouver une unique tuile permettant de paver le plan à elle seule, alors que dans les images ci-dessus, il suffisait d’assembler les motifs deux par deux pour obtenir une tuile pavant le plan.

Si l’on considère ce genre de pavage, il existe une infinité de manières de paver le plan.